Stabilité dynamique
Rappel : Travail élémentaire d'un couple
Dans le cas d'un couple inclinant appliqué brutalement , la carène prend une certaine vitesse et emmagasine ainsi une énergie telle qu’elle dépassera l'angle de gîte auquel elle se serait normalement arrêtée.
On sait que si un solide tourne sous l'action d'un couple de moment variable avec l'angle de rotation, le travail élémentaire du couple pour une rotation infiniment petite peut s'écrire :
\(dW=M(\theta)d\theta\)
Pour une rotation d'amplitude donnée, le travail du couple est alors:
\(W=\int M(\theta)d\theta\)
Ce résultat est applicable au bras de levier de redressement du navire:
\(W=\int P\cdot GZ(\theta)d\theta\)
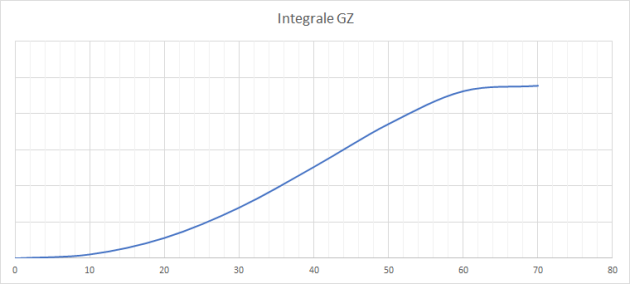
Cette quantité est proportionnelle à la réserve de stabilité et est représentée graphiquement par l'aire de la surface sous la courbe GZ.
Rappel : Variation d'énergie cinétique
On sait que la variation d'énergie cinétique d'un solide en rotation est égale à la somme des travaux des couples de forces extérieures, en considérant la valeur d'énergie cinétique à un instant t, on obtient :
\(E_{C_t}=\frac{1}{2}\cdot J\cdot\theta'^2\)
\(E_{C_t}\) est la valeur de l’énergie cinétique à l’instant t
\(J\) est le moment d’inertie du navire
\(\theta'\) est la vitesse angulaire
Application brutale d'un couple inclinant
Le navire étant initialement en équilibre sans gîte et en eau calme, on applique brutalement un couple inclinant transversale qui est ensuite maintenu, comme cela peut être le cas avec une violente rafale de vent traversier persistante.
On a donc à l’instant t:
\(\frac{1}{2}\cdot J\cdot \theta'^2=\int C_i (\theta)d\theta-\int P\cdot GZ(\theta)d\theta\)
Fondamental : \(Quantite E_c\not=\Delta E_c\)
La quantité d’énergie cinétique dépendra de \(\int C_i (\theta)d\theta-\int P\cdot GZ(\theta)d\theta\) alors que la variation d’énergie cinétique sera donc fonction de la dérivée de la fonction ci-dessus soit de la valeur de \(C_i(\theta)d\theta-P\cdot GZ(\theta)d\theta\).
Description physique du phénomène
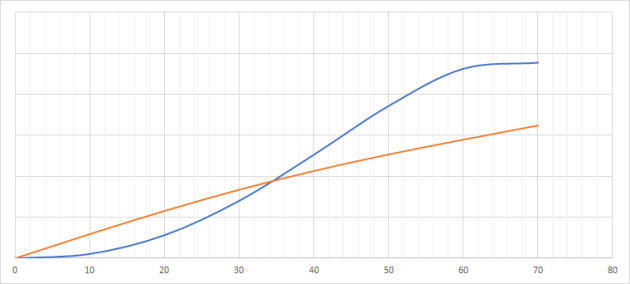
À partir de t=0 le couple inclinant est d'abord supérieur au couple de redressement, la variation d'énergie cinétique est donc positive, le mouvement est accéléré et le navire s'incline avec une vitesse d‘inclinaison croissante.
À un certain moment le couple inclinant est égal au couple de redressement la quantité d'énergie cinétique est maximale tout comme la vitesse d'inclinaison. On notera que cet angle correspond à l'angle d'inclinaison d'équilibre statique.
Le mouvement se poursuit donc mais cette fois le couple inclinant est inférieur au couple de redressement, la variation d'énergie cinétique est donc négative, le mouvement est ralenti et le navire continue à s'incliner mais avec une vitesse d'inclinaison décroissante.
Enfin arrive un moment où la quantité d’énergie cinétique s’annule, précisément lorsque:
\(\int C_i (\theta)d\theta=\int P\cdot GZ(\theta)d\theta\)
Graphiquement cela correspond à un angle d'inclinaison tel que les aires sous-tendues par les courbes représentatives du couple inclinant et du couple de redressement soient égales, soit approximativement 34° dans notre exemple.
Le navire est ensuite rappelé vers sa position d'équilibre par son couple de redressement et ce mouvement d'oscillation pourrait continuer indéfiniment en l'absence de frottement. En pratique du fait des résistances, le navire vient après quelques oscillations d'amplitude décroissantes se stabiliser à l'inclinaison d'équilibre statique.
D'un point de vue de la stabilité, un navire avec un propulseur éolien sera doublement impacté par la l'action du vent. En effet la présence d'un gréement induira nécessairement une élévation du centre de gravité, plus ou moins important selon le type de propulseur, et donc une diminution du \(GZ_{max}\), alors que l'augmentation de la surface vélique entraînera une sensibilité accrue à l'action du vent.
Remarque : Impact structurel
De manière générale , si les accélérations augmentent, les efforts aussi, ce qui peut nécessiter de renforcer les profils et les gréements associés.