Lignes de courant et trajectoires
Description d'Euler
C'est une description de l'écoulement qui consiste à établir à un instant \(t\) donné l'ensemble des vitesses associées à chacun des points de l'espace fluide. Ainsi, à chaque point M est associé une vitesse \(V_M(t)\) susceptible d'évoluer dans le temps. L'écoulement du fluide est alors décrit au moyen d'un ensemble de vecteurs vitesse appelé champ de vecteurs vitesse.
Sur la base de ce champ de vecteurs vitesse, on définit comme ligne de courant la courbe qui en chacun de ses points est tangente au vecteur vitesse. Au même titre que le champ de vecteurs vitesse, il s'agit donc d'une représentation de l'espace fluide susceptible d'évoluer dans le temps ; en conséquence, on prendra soin de dater les lignes de courant ainsi définies (ligne de courant passant par tel point à l'instant \(t\)).
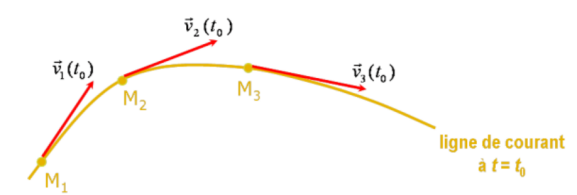
On voit que cette courbe peut être assimilée à une image instantanée de l'écoulement.
Description de Lagrange
Il s'agit d'une description de l'écoulement qui consiste à suivre dans l'espace fluide la position d'une particule choisie en fonction du temps. Il en découle la définition de la trajectoire d'une particule fluide : c'est l'ensemble des positions occupées successivement par une même particule.
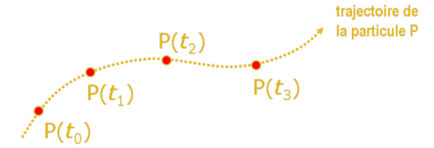
Remarque :
Il ne faut pas confondre ligne de courant et trajectoire. Ce sont deux notions fondamentalement différentes. En effet, si initialement (à \(t=t_0\)) une particule occupe un point \(M_0\), elle se dirigera naturellement dans la direction donnée par la ligne de courant passant par \(M_0\) à \(t_0\), mais à \(t_1> t_0\) cette même particule se trouvera en un point \(M_1\) appartenant à une ligne de courant définie à \(t_1\) et qui n'a a priori aucune raison d'être identique à celle définie à \(t_0\). Les deux courbes divergent donc dès que \(t> t_0\).
On pourrait comparer la description eulérienne à une photographie de l'écoulement, et la description lagrangienne à une prise de vue en travelling du mouvement d'une seule particule.
Ecoulement permanent
Un écoulement est qualifié de permanent (ou stationnaire) lorsque le champ de vecteurs vitesse de l'espace fluide qu'il occupe est statique : les vecteurs vitesse n'évoluent pas dans le temps. Les conséquences sont multiples :
les lignes de courant sont aussi statiques ;
les trajectoires coïncident avec les lignes de courant .
Dans un écoulement permanent, les trajectoires suivies par les particules du fluide sont donc constantes et se confondent avec les lignes de courant. On peut matérialiser celles-ci en soufflerie par exemple par l'introduction dans le fluide de fumées colorées.
