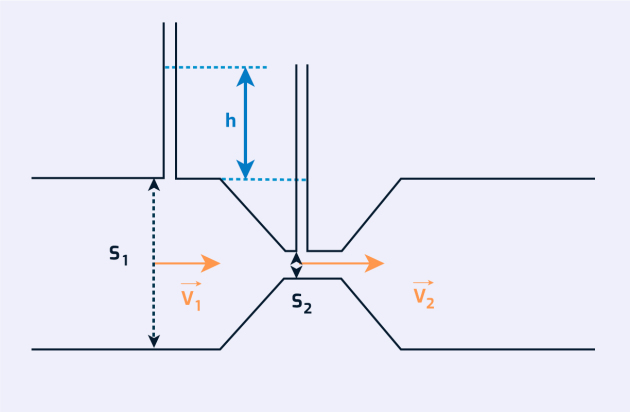
Exercice : Le tube de Venturi
Voyons maintenant au travers d'un exercice d'application comment les équations de Bernoulli et de conservation des masses peuvent s'articuler afin de donner un début d'explication à l'écoulement d'un fluide.
Considérons un tube convergent-divergent muni de prise de pression statique, l'un en amont du convergent(\(P_1\)), l'autre au niveau du col (\(P_2\)).
Un fluide quelconque s'écoule au travers de ce tube, de manière continue et uniforme.
Question
Exprimez la différence des pressions \(P_2-P_1\) en fonction de la vitesse \(V_2\) du fluide et des sections \(S_1\) et \(S_2\).
Indice
Utilisez la relation de Bernoulli en considérant une altitude constante. Pensez à la conservation du débit en volume pour « éliminer » \(V_1 \).
Solution
Soit \(P_1\) et \(P_2\) les pressions dans les sections \(S_1\) et \(S_2\) ; on obtient d'après l'équation de Bernoulli :
\(\frac{V_1^2}{2}+gz_1+\frac{P_1}{\rho}= \frac{V_2^2}{2}+gz_2+\frac{P_2}{\rho}\)
En considérant \(z_1=z_2\) on trouve :
\(\frac{V_1^2}{2}+\frac{P_1}{\rho}= \frac{V_2^2}{2}+\frac{P_2}{\rho}\) (1)
Egalement on sait que :
\(S_1\cdot V_1=S_2\cdot V_2\) et donc que :
\(V_1=\frac{S_2\cdot V_2}{S_1}\) (2)
En réinjectant la valeur de \(V_1\) dans (1) on trouve :
\(P_2-P_1= \frac{V_2^2}{2}\cdot \rho\cdot \left( \left(\frac{S_2}{S_1}\right)^2-1\right)\)
Question
En considérant \(V_2\) et \(\rho\) strictement positifs et \(S_2\)<\(S_1\), que pouvez-vous en déduire concernant la valeur de cette différence de pression ?
Solution
Si \(S_2\)<\(S_1\), alors :
\(\frac{S_2}{S_1}<1\)
ou encore :
\(\left(\frac{S_2}{S_1}\right)^2-1<0\)
En considérant que \(V_2\) et \(\rho\) strictement positifs, il vient :
\(P_2-P_1<0\) et donc finalement que :
\(P_2<P_1\)
Autrement dit si la section de la veine de fluide diminue, la pression au niveau du col diminuera également.
L'effet Venturi, qui est donc une application possible du théorème de Bernoulli, est utilisé dans de nombreuses application nécessitant de créer une force d'aspiration importante, comme dans le condenseur d'une installation vapeur ou une installation d'extinction incendie à mousse par exemple.