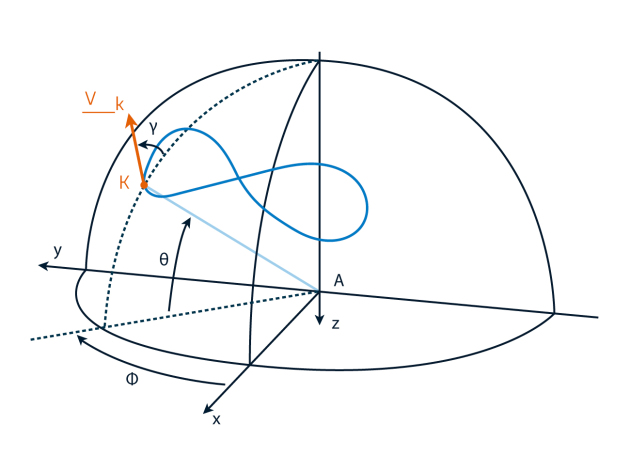Exercice : Saurez vous prévoir le vol d'un profil aérien ?
Pourquoi modéliser le vol d'un profil aérien ?
Si' l'on a pu étudier le vol de profils ayant des surfaces relativement faibles au cours des dernières années, les données et retours d'expériences concernant les profils « géants » sont beaucoup moins nombreux.
En effet, leur mise en œuvre dans le cadre de la propulsion de navires de charges est récente et induit des ordres de grandeurs biens différents de ceux rencontrés jusqu'alors.
Ainsi en va-t-il des forces développées, qui passent de quelques dizaines de kilogrammes à plusieurs tonnes avec toutes les conséquences que l'on peut imaginer sur la structure des profils, l'échantillonnage des matériaux, les actionneurs...etc
Il en va de même des systèmes de pilotage, qui doivent assurer une évolution sûre et optimisée du profil en tenant compte d'une multitude de paramètres.
Afin d'être en mesure de développer de tels systèmes il est donc nécessaire de pouvoir prédire le comportement du profil en modélisant le vol.
Modélisation de la trajectoire
Considérons un profil aérien évoluant dans sa fenêtre de vol selon une trajectoire prédéfinie.
Le vecteur rouge est le vecteur vitesse du profil
Le vecteur vert est le vecteur de position du profil
Question
Pour un vent et un profil donné, de quoi dépend la valeur du vent apparent perçu par ce profil?
Indice
\(AWS=\frac{V_{WR}\cdot\cos(\phi)\cdot\cos(\theta)}{\sin(\epsilon)}\)
Avec
\(AWS\) le vent apparent perçu par le profil
\(V_{WR}\) le vent relatif à l'altitude du profil ; il est mesuré ou au moins estimé et est donc connu
\(\phi\) l'azimut du vecteur position du profil ;
\(\theta\) l'élévation du vecteur position du profil ;
\(\epsilon\) l'angle de finesse aérodynamique ; il dépend du profil utilisé et est également connu
Solution
Position du profil dans la fenêtre de vol
D'après cette formule, la valeur du vent apparent \(AWS\) ne dépend alors que de la position du profil dans la fenêtre de vol.
Question
Que pouvez-vous en déduire en ce qui concerne la force aérodynamique ?
Indice
\(Fa=\frac{Cp\cdot\rho\cdot S\cdot AWS^2}{2\cdot\cos(\epsilon)}\)
Avec :
\(Cp\) le coefficient de portance du profil
\(\rho\) la masse volumique de l'air
\(S\) la surface du profil
\(AWS\) la vitesse du vent apparent
\(\epsilon\) l'angle de finesse aérodynamique
Solution
Force aérodynamique
On peut en déduire que, dans ce cas, la valeur de la force aérodynamique générée par le profil ne dépend que de la position du profil dans la fenêtre de vol.
Remarque : Direction de la force aérodynamique
Les lignes étant considérées comme droites, la force aérodynamique est colinéaire au vecteur position. Autrement dit, la force aérodynamique est égale et opposée à la force de traction exercée sur les lignes.
Nous connaissons donc désormais la valeur de la force de traction pour chaque point de la trajectoire.
Question
\(AWS\) et \(\overrightarrow{V_{WR}}\) étant connus, que peut-on déduire de la relation vectorielle suivante ?
\(\overrightarrow{V_K}=\overrightarrow{V_{WR}}-\overrightarrow{AWS}\)
Avec :
\(\overrightarrow{V_K}\) le vecteur vitesse du profil
\(\overrightarrow{V_{WR}}\) le vent relatif à l'altitude du profil ; il est normalement mesuré ou estimé
\(\overrightarrow{AWS}\) le vecteur vent apparent perçu par le profil
Indice
La direction du vecteur vitesse du profil \(\overrightarrow{V_K}\) est connue puisqu'il est tangent à la trajectoire suivie par le profil, qui est elle-même prédéfinie.
Solution
Direction du vent apparent
Il est possible de déduire la norme du vecteur vitesse du profil de l'équation ci-dessus.
Question
Quel intérêt ?
Solution
Force de traction
La connaissance de la norme du vecteur vitesse du profil permet, en intégrant les valeurs de la force aérodynamique prises au cours de la trajectoire, d'obtenir la force de traction moyenne générée par le profil au cours de cette trajectoire.
En projetant cette valeur sur les axes du navires, il est possible d'obtenir les composantes propulsives et de dérive pour une trajectoire donnée.
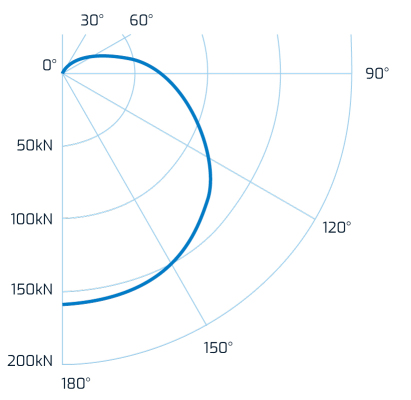
Fondamental : Allures de portant
On peut notamment voir qu'un profil aérien est généralement plus performant aux allures de portant qu'à celles de travers.
Ceci est notamment dû à l'orientation de la fenêtre de vol qui reste toujours perpendiculaire au vent apparent.