Théorème de Kutta- Joukowski
Pourquoi un énième théorème ?
Ce théorème date du début du 20° siècle, à une époque où il était nécessaire de simplifier les équations régissant les écoulements fluides de manière à pouvoir calculer les forces en jeu sur un profil.
Il permet encore de nos jours d'expliciter relativement simplement la modification du champ de vitesse autour d'un profil.
Principe du théorème
La viscosité est considérée comme nulle, et ce même à proximité du profil.
Autrement dit la couche limite est considérée comme inexistante de manière à se retrouver dans les conditions d'un écoulement en fluide parfait.
Rappel : Fluide parfait= paradoxe de d'Alembert
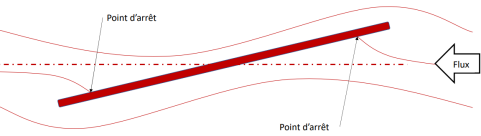
L'étude des lignes de courant en fluide parfait nous montre une ligne de séparation qui aboutit au point d'arrêt et qui réapparaît à l'arrière, à l'endroit où les deux flux se rejoignent, créant alors un écoulement symétrique.
A ce stade, nous nous retrouvons donc confronté au paradoxe de d'Alembert.
La circulation périphérique
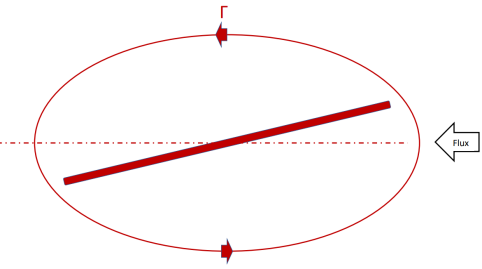
Dans la réalité, la viscosité est bien présente. Afin de tenir compte de ses effets, Kutta et Joukowski ont eu l'idée de superposer au champ de vitesse représenté par les lignes de courant, une circulation \(\Gamma\) autour de l'objet, dont la vitesse s'ajoute sur l'extrados et se retranche sur l'intrados.
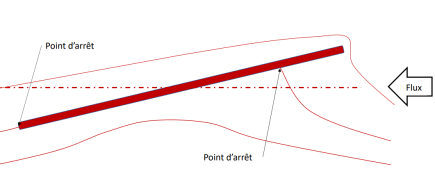
En faisant ainsi, on se rend compte que l'on se retrouve dans les même conditions qu'un écoulement réel, avec viscosité donc.
Le point d'arrêt= circulation périphérique
La position du point d'arrêt permet de caractériser cette circulation et donc indirectement la force résultante. Celui-ci se décale vers l'aval au fur et à mesure de l'augmentation de l'incidence.
Remarque : Temps de transit égal= faux ! ! !
Une explication souvent donnée à la modification du champ des vitesses, est que le fluide passant sur l'extrados doit parcourir une distance plus grande que celui passant sur l'intrados sur une même durée.
Ainsi cela le contraindrait à accélérer afin d'arriver en même temps que le fluide de l'intrados au niveau du bord de fuite.
Or cela est inexacte, comme nous pouvons le constater sur la vidéo suivante :
Complément : Le tourbillon initiateur
Si on considère initialement un écoulement sur un profil avec un bord de fuite aigu et une incidence positive, les deux points d'arrêt se trouvent dans les mêmes positions que dans le cas d'un écoulement de fluide parfait.
Quand l'air qui passe sous l'intrados atteint le bord de fuite il doit contourner celui-ci pour aller vers le point d'arrêt aval.
À cause du rayon de courbure très faible, la vitesse devrait être localement infinie.
À défaut de vitesse infinie, il y a une vitesse importante qui crée sur l'extrados, près du bord de fuite, un tourbillon appelé tourbillon initiateur.
La circulation de ce tourbillon est équilibrée par celle du tourbillon attaché au profil. Lorsque la première croît, la seconde croît dans les mêmes proportions, ce qui déplace le tourbillon initiateur vers le bord de fuite où il quitte le profil avant d'être dissipé par viscosité.
À ce stade, le positionnement du point d'arrêt au bord de fuite, qui constitue la condition de Kutta, a stabilisé l'écoulement.
Fondamental : Modification champ vitesses= modification champ pression= portance
En résumé, c'est bien la mise en place d'une circulation de vitesse périphérique qui créé une dissymétrie des champs de vitesse et par là même une modification des champs de pression sur les deux faces, à l'origine de la force de portance.
Complément : Les équation de Navier-Stokes
Le principal objectif de cette équation est de décrire le mouvement des fluides. Puisqu’un fluide peut être un liquide ou un gaz, on comprend que l’équation de Navier-Stokes concerne tout un tas de choses qui nous entourent.
Vous trouverez dans ce lien des informations complémentaires quant à ces équations fondamentales.