Expression des forces
Définition : Formule mathématique
Afin d'étudier le comportement d'un profil, on ramène l'ensemble de ces forces à des coefficients de telle sorte que la force globale développée par le profil soit de la forme :
\(F=\frac{1}{2}\cdot\rho\cdot S\cdot C\cdot V^2\)
Avec :
\(\rho\) la masse volumique du fluide ;
\(S\) la surface en contact avec le fluide ;
\(C\) coefficient de portance (\(C_L\) pour Lift) ou de traînée (\(C_D\) pour Drag) selon l'axe concerné ;
\(V\) la vitesse de l'écoulement.
Exemple : Représentation graphique
La courbe donnant la valeur de \(C_L\) en fonction de \(C_D\) à divers angles d'incidence est une polaire de Eiffel.
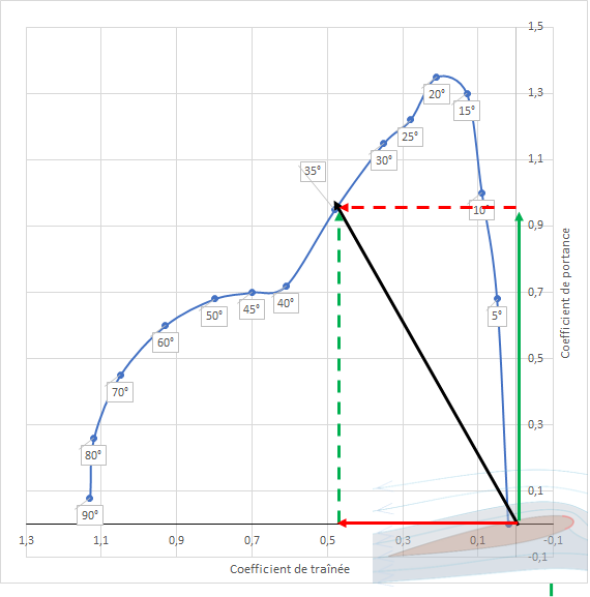
Les valeurs du coefficient de portance sont portées en ordonnée.
Les valeurs du coefficient de trainée sont portées en abscisse.
Le vecteur noir représente la résultante des force de portance et de trainée pour une incidence donnée (ici 35°).
Description de la courbe
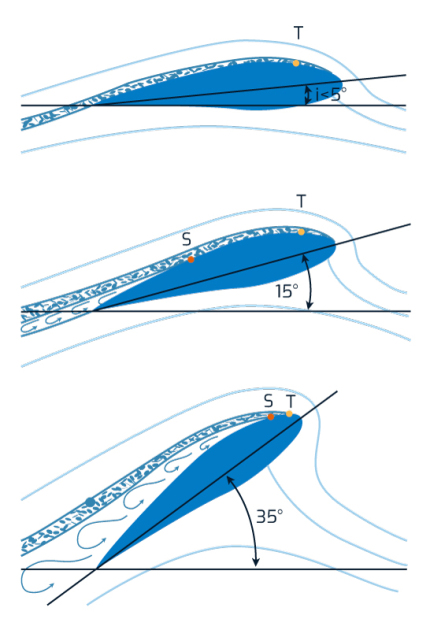
Jusqu'à un angle de 5°, le point de transition avance régulièrement du 1/3 au 1/10 du profil.
Dans cette partie de la polaire, la portance est proportionnelle à l'incidence. La traînée est, quant à elle, proportionnelle au carré de la portance.
T est le point de transition entre l'écoulement laminaire et l'écoulement turbulent
S est le point de séparation de la couche limite de la surface du profil
A partir de 5°, la couche limite commence à se décoller du profil. La traînée augmente et le point de séparation \(S\) avance.
A 19° il rejoint le point de transition \(T\).
Les remous recouvrent alors la quasi totalité de la surface du profil, provoquant la chute brutale du coefficient de portance.
On dit que le profil décroche.
Remarque : Transition pas ponctuelle
La transition, n'est pas ponctuelle mais s'étend sur une zone plus ou moins grande qui peut atteindre 20% de la longueur du profil en arrière du point de transition théorique.
Attention : Exemple
Les valeurs indiquées correspondent à celles de la courbe donnée en exemple et ne constituent pas des valeurs de référence.
Nombre de Reynolds
La valeur des forces unitaires développées sur la surface du profil étant essentiellement fonction de la qualité des écoulements, on comprend que ceux-ci seront d'autant meilleurs que le point de séparation en sera plus reculé.
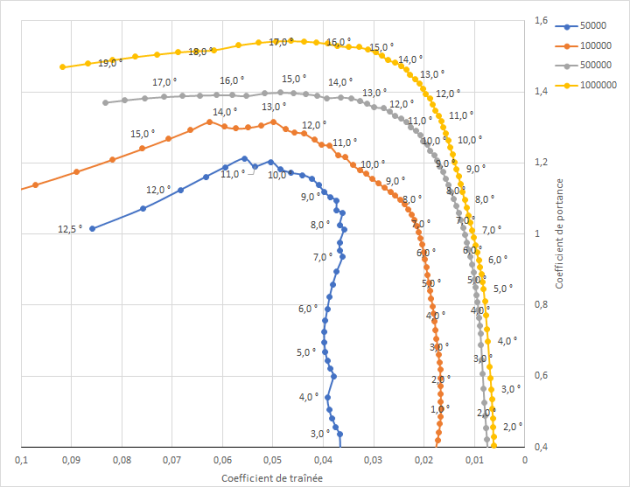
Les valeurs des coefficients de portance et de traînée correspondent à ceux d'un profil NACA 2414.
Les données en degré correspondent à l'angle d'incidence du profil pour le point considéré.
On peut voir sur le graphique que la valeur du nombre de Reynolds influera essentiellement sur la valeur de \(C_L\), celle de \(C_D\) restant sensiblement constante.
Remarque : Traînée jamais nulle
On remarque que le coefficient de portance peut être nul ce qui n'est pas le cas de celui de trainée. En effet, le plan possède dans la réalité une certaine épaisseur qui induit nécessairement une force de trainée, et ce quelque soit l'incidence.
Définition : Coefficient de finesse
On définit le coefficient de finesse comme étant le rapport entre le coefficient de portance et celui de trainée tel que :
\(Cf=\frac{C_L}{C_D}\)
Avec :
\(C_L\) : coefficient de portance
\(C_D\) : coefficient de trainée
Il permet de caractériser la capacité d'un profil dans un écoulement donné à créer une force résultante orientée perpendiculairement au flux, autrement dit, à générer une force de portance.
La finesse maximum correspond à la tangente à l'origine sur une polaire de Eiffel.
Coefficient de finesse= indication direction de la force résultante
La finesse ne permet d'apprécier que la direction de la force générée par le profil, et non sa norme.
Compromis
Pour de faibles angles d'incidence, la résultante de \(C_L\) et \(C_D\) est bien orientée mais de valeur relativement faible.
En augmentant légèrement l'incidence la force résultante est plus importante bien que légèrement moins bien orientée.
Dans le cas où l'on chercher à améliorer la performance d'un profil, il faudra considérer à la fois la valeur de la finesse et celle de la force résultante afin d'adopter un compromis satisfaisant.