Résistance à l'avancement
Définition : Résistance de remorquage
La résistance de remorquage est la résistance à l'avancement totale d'un navire.
Elle se compose de la résistance hydrodynamique à laquelle on ajoute la résistance aérodynamique :
\(R_{rem}=R_t= R_{hydro}+R_{aero}\)
Avec :
\(R_t\) la résistance à l'avancement totale
Remarque : Résistance aérodynamique \(\simeq0\)
En première approximation cette résistance est souvent négligée du fait de sa valeur relativement faible devant la résistance hydrodynamique. On obtient donc :
\(R_{hydro}\simeq R_t\)
Exemple : Puissance de remorquage d'un navire de charge moyen
A titre d'exemple, un navire de charge de taille moyenne (11 000 tonnes de déplacement) et entre 130 m et 140 m de longueur nécessite environ 1 100 kW (efficace à la coque) pour être propulsé à une vitesse de 11 nœuds.
Hypothèse de Froude
La résistance totale à l'avancement d'un navire en eau calme peut se décomposer en considérant une séparation géométrique de la physique dans chaque partie de l’écoulement :
\(R_T=R_w (Fn)+R_v(Re)\)
Avec :
\(R_v\) la résistance visqueuse, représentée par le nombre de Reynolds \(Re\)
\(R_w\) la résistance de vague, représentée par le nombre de Froude \(Fn\)
Définition : Nombre de Froude
En se basant sur les lois de similitude de la mécanique générale et ses propres observations des systèmes de vagues engendrées par des modèles de tailles différentes, Froude a défini le nombre adimensionnel qui porte son nom:
\(Fn=\frac{V}{\sqrt{g\cdot L}}\)
Avec :
\(V\) la vitesse
\(g\) l'accélération de la pesanteur
\(L\) une longueur de référence
Exemple : Nombres de Froude
Ci-dessous nous trouverons un tableau indiquant différents \(Fn\) en fonction de la taille et la vitesse du navire considéré :
L (m)/V (kts) | 2 nds | 4 nds | 6 nds | 8 nds | 10 nds | 12 nds | 14 nds | 16 nds | 18 nds | 20 nds | 22 nds | 24 nds |
5 m | 0.147 | 0.294 | 0.441 | 0.588 | 0.735 | 0.881 | 1.028 | 1.175 | 1.322 | 1.469 | 1.616 | 1.763 |
10 m | 0.104 | 0.208 | 0.312 | 0.416 | 0.519 | 0.623 | 0.727 | 0.831 | 0.935 | 1.039 | 1.143 | 1.247 |
15 m | 0.085 | 0.170 | 0.254 | 0.339 | 0.424 | 0.509 | 0.594 | 0.679 | 0.763 | 0.848 | 0.933 | 1.018 |
20 m | 0.073 | 0.147 | 0.220 | 0.294 | 0.367 | 0.441 | 0.514 | 0.588 | 0.661 | 0.735 | 0.808 | 0.881 |
25 m | 0.066 | 0.131 | 0.197 | 0.263 | 0.328 | 0.394 | 0.460 | 0.526 | 0.591 | 0.657 | 0.723 | 0.788 |
30 m | 0.060 | 0.120 | 0.180 | 0.240 | 0.300 | 0.360 | 0.420 | 0.480 | 0.540 | 0.600 | 0.660 | 0.720 |
35 m | 0.056 | 0.111 | 0.167 | 0.222 | 0.278 | 0.333 | 0.389 | 0.444 | 0.500 | 0.555 | 0.611 | 0.666 |
40 m | 0.052 | 0.104 | 0.156 | 0.208 | 0.260 | 0.312 | 0.364 | 0.416 | 0.467 | 0.519 | 0.571 | 0.623 |
45 m | 0.049 | 0.098 | 0.147 | 0.196 | 0.245 | 0.294 | 0.343 | 0.392 | 0.441 | 0.490 | 0.539 | 0.588 |
50 m | 0.046 | 0.093 | 0.139 | 0.186 | 0.232 | 0.279 | 0.325 | 0.372 | 0.418 | 0.465 | 0.511 | 0.557 |
Catégories de navires
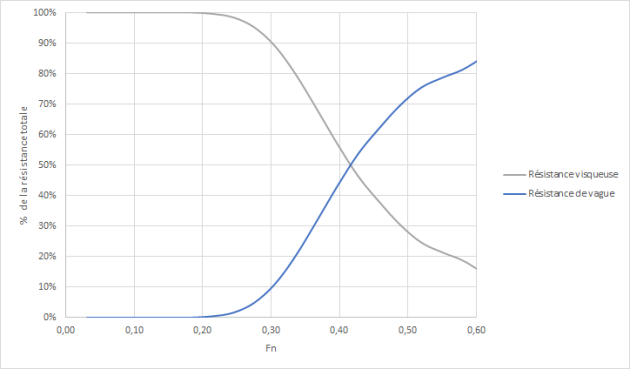
On peut, grâce au nombre de Froude, répartir les navires suivant 4 grandes catégories.
On peut noter qu'aux alentours de Fn=0,4, la résistance de vague devient largement prédominante dans la résistance totale à l'avancement du navire.
Fn< 0.27
À faible vitesse, les vagues d'accompagnement ont une longueur d'onde inférieure à la longueur du navire.
On peut alors admettre que la résistance de vague est relativement faible, tandis que la résistance de frottement est nettement prédominante (de l'ordre de 60 à 90% de la résistance totale selon Fn et la forme du flotteur).
Au-delà, la résistance de vague devient progressivement de plus en plus importante avec la vitesse.
Exemple : Porte-conteneur
Un porte-conteneur de 300 m de long évoluant à 20 nœuds à un \(Fn\simeq\) 0,18.
0.27< Fn< 0.4
Lorsque celle-ci augmente la longueur d'onde des vagues augmente jusqu'à correspondre approximativement à la longueur du navire, qui est alors en quelque sorte porté par une seule onde constituée d'une crête à l'avant, un creux au milieu, et une crête à l'arrière.
La résistance de vagues devient sensiblement plus grande que la résistance de frottement.
Exemple : Chalutier
Un chalutier de 24 m navigant à 12 noeuds à un \(Fn\simeq\) 0,4
0.4< Fn< 0.7
Si la vitesse augmente encore, la crête arrière s'éloigne du navire, l'arrière n'est alors plus porté par la vague arrière, mais par la pente de la vague entre les 2 crêtes.
Le navire se trouve en situation cabrée, très défavorable du point de vue de la résistance à l'avancement.
La résistance de vague est alors largement prédominante (de l'ordre de 70 à 85% de la résistance totale).
Fn> 0.7
Enfin si la vitesse continue à augmenter, le navire peut à la limite se retrouver entièrement porté par sa vague avant, il est alors en situation de planning. On observe que dans cette situation le navire n'est plus porté sur toute sa longueur effective mais seulement sur sa partie arrière.
Remarque : Forme de la carène
Toutes les carènes ne sont pas capables de planer : les bateaux lourds buttent sur le "mur de vagues" avec un nombre de Froude qui ne dépasse pas 0,4.
On peut augmenter la puissance d'un chalutier de 24 m mais il ne dépassera guère les 13 nœuds que lui autorisent sa longueur de flottaison.
Fondamental : Navires à déplacement
On retiendra que jusqu’à un Fn=0,4, les navires considérés sont dits à “déplacement” tandis qu'au-delà seuls les navires relativement légers dotés de puissance propulsive importante avec des formes porteuses, c'est à dire présentant une grande surface plate principalement à l'arrière, sont concernés.
Remarque : Une autre décomposition possible
La décomposition présentée ci-dessus ne doit pas être confondue avec celle utilisée par W. Froude, et encore utilisée de nos jours dans de nombreux bassins d’essais, qui consiste à supposer que la résistance totale se décompose en deux termes indépendants :
Une résistance de frottement \(R_f\)
Une résistance résiduaire \(R_r\) qui contient toute la résistance de vagues, et une partie des effets liés à la viscosité, comme par exemple la résistance de remous. La résistance de vague est généralement prédominante sur les autres.
Par identification on obtient :
\(R_v+R_w= R_f+R_r\)
Ces différentes décompositions de la résistance à l'avancement fournissent le même résultat pour la résistance totale, par contre chaque terme pris isolément est différent.