Résistance de forme
Paradoxe de d'Alembert
Si nous considérons un corps immergé totalement dans un fluide parfait de pression \(P_0\) uniforme, nous observerons qu'à l'avant de celui-ci, dans la zone où les lignes de courant s'infléchissent pour s'écarter, le gradient de pression \(P_t=P_0+\Delta P\) s’accroît.
Mais aussitôt la pression diminue pour atteindre une valeur \(P_0-\Delta P\) minimum au maximum de la largeur du corps. En arrière de ce point la pression remonte progressivement à \(P_0+\Delta P\) maximum pour revenir à \(P_0\) en arrière du corps.
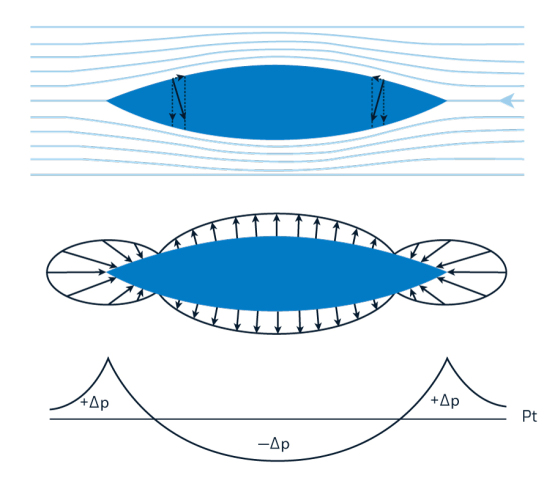
Dans un écoulement de fluide parfait il n'y a pas de résistance de forme car les écoulements s'effectuent de manière symétrique et les résultantes de pression avant et arrière s'annulent.
Les composantes horizontales des pressions sur l'avant et l'arrière du corps sont de sens contraire et s'annulent, dans un fluide parfait un corps ne rencontre donc pas de résistance à son déplacement. C'est le paradoxe de d’Alembert.
Fluide parfait ou réel ?
Mais dans un fluide réel, la couche limite, éventuellement la séparation, viennent modifier la forme virtuelle du corps et altérer les mouvements du fluide.
Si l'écoulement sur la partie avant du corps reste proche de l'écoulement dans les fluides parfaits avec création d'une force axiale dirigée vers l'arrière, il n'en est rapidement plus de même dès que l'on recule vers l'arrière et la résultante des composantes axiale ne peut plus alors être nulle.
Définition : La résistance de forme
La différence entre la résistance mesurée et la résistance de frottement calculée grâce à \(C_f\) est la résistance de forme :
\(R_x=Pd\cdot S\cdot C_x\)
Avec :
\(C_x\) un coefficient de forme qui reste constant dans un écoulement donné, quel que soit le nombre de Reynolds donc, mais qui variera considérablement selon la forme du corps.
Le coefficient de résistance total
Le coefficient de résistance totale, \(C_t\), égal à la somme de \(C_f\) et \(C_x\), évoluera donc selon la forme mais également le type d’écoulement présent.
Dans le cas d'un corps profilé la part de la résistance de forme dans la résistance totale est faible et cela d'autant plus que la section frontale est elle-même réduite.
Ainsi pour un profil de rapport épaisseur/longueur de 1:16, l'augmentation de résistance par rapport à la résistance de frottement n'est que de 8 % alors qu'elle atteint 30 % pour un profil deux fois plus épais.
Il ne faudrait cependant pas en conclure qu'il faut toujours aplatir au maximum la section, mais plutôt privilégier le rapport longueur/ épaisseur.
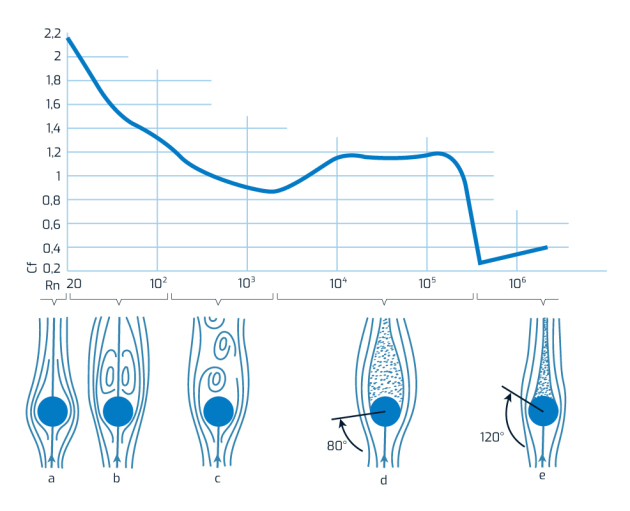
Nombre de Reynolds critique
On constate qu'à partir d'une certaine vitesse d'écoulement le mouvement turbulent atteint toute la couche limite.
On a atteint le nombre de Reynolds critique qui correspond à une chute brutale du coefficient de résistance \(C_t\).
On voit ici que le nombre de Reynolds critique se situe aux alentours de 500 000. A partir de cette valeur, le coefficient de résistance diminue brutalement.