Résistance de remous
Définition :
Il s'agit de la résistance créée suite à des phénomènes de décollement ou de tourbillonnement de la couche limite d'un profil placé dans un écoulement fluide.
Un profil n'est pas une surface plane
L'écoulement sur une surface plane est relativement simple à appréhender. En revanche, sur un profil courbe, certaines modifications vont apparaître, notamment dues à la variation de la pression au niveau de la surface au contact du fluide.
Définition : Le coefficient de pression
Il s'agit d'un coefficient adimensionnel que l'on retrouver dans l’étude de la distribution des pressions autour de corps placés dans un écoulement de fluide.
Il a pour expression :
\(C_p=\frac{P-P_\infty}{\frac{1}{2}\cdot \rho_\infty \cdot V_\infty^2}\)
Avec :
\(P\) la pression au point considéré ;
\(P_\infty\) la pression du milieu ambiant, non impacté par la présence du profil,
\(\rho_\infty\) la masse volumique du fluide ambiant,
\(V_\infty\) la vitesse du fluide ambiant.
Sa valeur est maximale et égale à 1 au point d'arrêt.
La variation de ce coefficient représente donc l'écart de pression entre le milieu ambiant et la surface du profil.
La pression le long d'un corps profilé fluctue
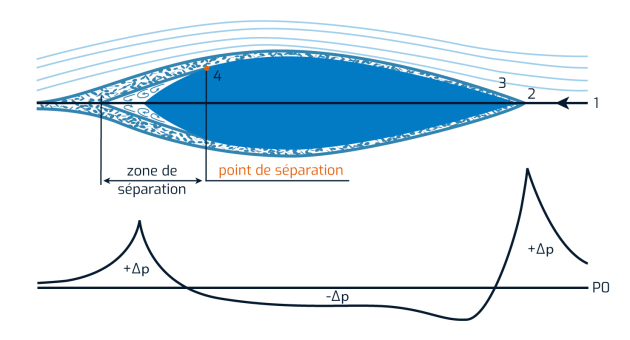
On sait que dans un fluide venant à l'encontre d'un corps profilé la pression \(P_t\) sera égale à \(P_0 + P_d\).
À l'approche de la rencontre du corps les lignes de courant seront déviées de part et d'autre et la pression \(P_t\) sera augmentée d'une quantité \(\Delta P\). Mais dès que ces lignes infléchiront leurs courses dans l'autre sens \(\Delta P\) deviendra négatif.
A l'arrière du corps profilé, tant que la pression \(P_t-\Delta P\) restera suffisamment élevée, les filets resteront collés à la surface.
En (2), la pression totale, qui est égale à la somme de la pression dynamique et statique, atteint un maximum ;
En (3), les lignes de courant se resserrent : la vitesse augmente et la pression diminue ;
En (4), les lignes de courant s'écartent : la vitesse diminue et la pression augmente, à tel point, qu'elle devient plus grande que la pression statique, ce qui provoque un décollement de la couche limite.
La couche limite peut se séparer du profil
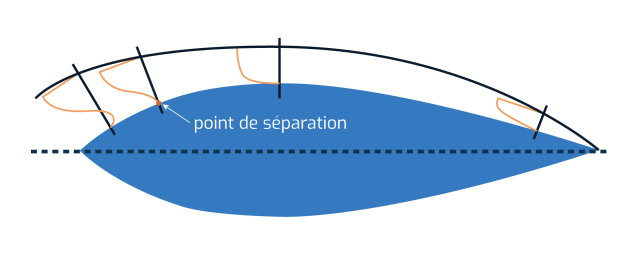
Dès que la pression \(P_t-\Delta P\) ne sera plus suffisante (si les formes d’arrière se modifient trop brutalement par exemple) la couche limite se décollera à partir d'un point appelé point de séparation.
Dans la zone de séparation entre la couche limite et l'arrière du corps se formera alors un ensemble de tourbillons et de contre-courants.
Il s'en suivra un accroissement de résistance dont le coefficient sera cependant à peu près constant quel que soit le nombre de Reynolds et la vitesse. Par contre on comprendra facilement que l'apparition de la séparation et la position du point de séparation dépendront de la valeur de \(P_t-\Delta P\) .
De chaque côté de cette zone de séparation l'écoulement continuera à s'effectuer comme si celle-ci constitue est un prolongement du corps.
La séparation a lieu lorsque le gradient de vitesse s'inverse, ce qui peut se visualiser ici par une inflexion de la courbe vers l'avant du profil.
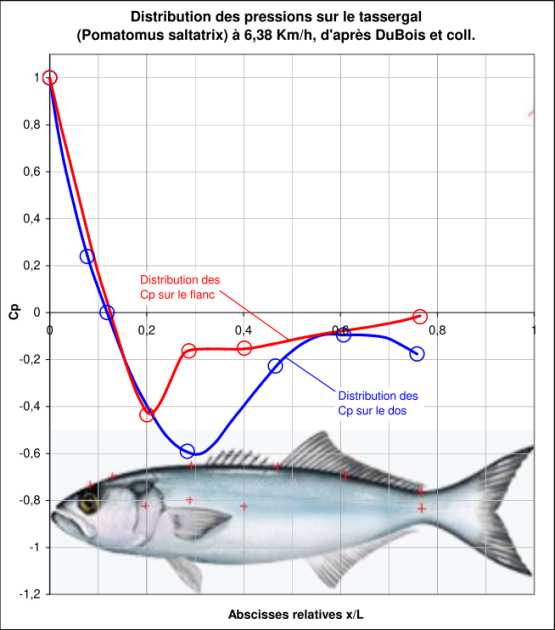
Exemple : La distribution des pression sur les corps des poissons
Les yeux des poissons sont placés très près du point où la pression est nulle, de sorte qu'ils peuvent nager sans que leurs globes oculaires soient distordus par la surpression ou la sous-pression due à la vitesse.
De même, l'ouverture de leurs ouïes est placée dans la zone de pression minimale afin d'activer la circulation d'eau depuis l'intérieur des ouïes.
La ventilation
Si maintenant nous considérons un corps profilé non plus entièrement plongé dans un fluide, de pression \(P_0\) uniforme, mais à cheval sur l’eau et l’air.
La pression \(P_0\) dépendra de la profondeur d’immersion et sera alors la somme de la pression atmosphérique \(P_a\) et de la pression hydrostatique \(P_h\).
\(P_h\) et par conséquent \(Pt-\Delta P\) diminuant vers la surface, le point de séparation avancera.
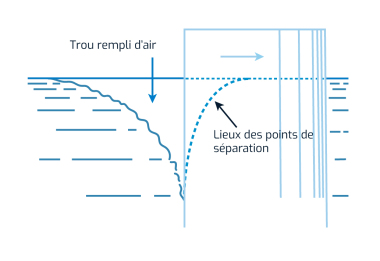
Si le corps est entièrement sous la surface mais à une distance assez faible la pression \(Pt-P_0\) pourra être assez basse pour que des bulles d'air puissent être attirées depuis la surface, c'est le phénomène que l'on appelle aération ou ventilation.
La ventilation est un phénomène que l'on rencontrera sur les hélices et les foils, où on la confond souvent avec la cavitation.
La cavitation
Si l'on suppose maintenant que le corps est immergé suffisamment profondément pour que la ventilation ne puisse se produire et que la pression au contact de la couche limite tombe à une valeur proche de zéro et inférieure à la tension de vapeur, il se forme dans l'eau des bulles qui se remplissent immédiatement de vapeur d'eau ou de gaz exactement comme lorsqu'on fait bouillir de l'eau.
Le phénomène, appelé cavitation, équivaut à ce qui se passe lorsque l'on porte de l'eau à une altitude élevé ; la diminution de la pression atmosphérique abaisse la température d’ébullition.
Les bulles qui se forment implose rapidement avant de se reformer selon un processus trop long à expliquer ici mais qui provoque des accroissements alternatifs de pression locale entraînant une érosion rapide de la surface du corps.
Remarque : La super cavitation
La cavitation peut se développer sous la forme d'une véritable feuille couvrant partiellement ou totalement la surface et se refermant en arrière de celle-ci. On évite ainsi l'érosion et l'écoulement s'effectue autour de la cavité sans présence d'une couche limite, et donc en l'absence de tout frottement de surface.
Ce phénomène est notamment mis en œuvre sur les hélices tournant à grandes vitesses avec des angles d'incidence très importants.